Lekce 3. Tradiční násobení z hlavy

Násobení přirozených čísel ve sloupci – jedná se o metodu, která vám umožní vynásobit libovolná víceciferná čísla bez kalkulačky. Pro použití této metody v praxi je třeba znát pravidla pro její aplikaci. Pojďme se blíže podívat na násobení různých čísel v teorii a na příkladech.

Základní principy násobení sloupci

Abyste tuto metodu násobení úspěšně používali, je třeba si pamatovat řadu matematických pravidel:

• Nejprve je potřeba znát násobilku nazpaměť a používat ji bez přemýšlení.
• Za druhé, nezapomeňte na pravidla násobení nulou. Nula se často vyskytuje ve dvou- a tříciferných číslech, což znamená, že bude fungovat jako jeden z činitelů.
• Pamatujte, že [x krát 0 = 0]
• Číslem x rozumíme jakékoli přirozené číslo.
• Než začnete řešit úlohy zahrnující násobení ve sloupcích, je vhodné si připomenout pravidla sčítání ve sloupcích a procvičit si sčítání čísel.
• Zopakujte si koncept hodnosti a porovnávání libovolných přirozených čísel.

Jak zapsat činitele při řešení úloh na násobení ve sloupcích

Klíčem k správnému vyřešení úlohy je schopnost správně zapsat výraz do sloupce. Zde se držíme následujících pravidel:

1. První násobitel se zapíše jako číslice, která má vyšší číslici.
2. Druhý násobitel je zapsán ve druhém řádku (pod prvním násobitelem). Je důležité přesně dodržovat vzorec shodných číslic. To znamená, že desítky se píší pod desítky, jednotky pod jednotky a nic jiného.
3. Poté, co jste všechny faktory napsali jeden pod druhý, je třeba nakreslit vodorovnou čáru, která je oddělí od odpovědi.

Podívejme se na příklad, jak takový výraz zapsat.

V příkladu vidíme, jak se dodržují místa při násobení čtyřmístného čísla trojmístným.

Abyste se naučili násobit ve sloupci, musíte pochopit, jak k násobení dochází a jak se zapisuje výsledek. Začněme násobením víceciferného dělitele jednociferným dělitelem.

Jak vynásobit dvouciferná čísla ve sloupci jednocifernými čísly

Pokud potřebujete vyřešit příklad násobení víceciferného přirozeného čísla jednociferným, můžete snadno použít tuto metodu. Postup řešení si ukážeme níže.

Podívejme se na algoritmus akcí:

1. Činitele zapisujeme do sloupce, přičemž přesně dodržujeme číslice. Jednotky píšeme pod jednotky, tedy 2 pod 4.
2. Násobíme je po řadě, přičemž dbáme na číslici. Nejprve násobíme dvěma jednotkami, pak desítkami, pak stovkami. Výsledek zapíšeme pod čáru.

Za zmínku stojí, že vzorek obsahuje čísla, jejichž násobení nepřesahuje 10. Pokud při násobení dostaneme dvouciferný výsledek, zapíšeme si pouze jednotky. Desítky si zapamatujeme a přičteme je k výsledku, který dostaneme při násobení další číslice. Pokud počet číslic skončil a existují nezapočítané desítky, jednoduše se zapíší jako číslice nejvíce vlevo.

Násobení ve sloupcích s nulami

Pokud potřebujeme vyřešit matematický problém, kde jeden z činitelů končí nulami, budeme muset jednat trochu jinak. Podívejme se na konkrétní příklad.

Podmínka: musíme vynásobit 5400 číslem 7.

První věc, kterou musíte udělat, je správně napsat výraz:

[začít časy začínají 5400 7 konec začátek řádku konec konec ]

Zde je nutné dbát na to, aby multiplikátor nebyl zapsán pod nulami.

Dalším krokem při řešení úlohy ve sloupci je násobení bez započítání nul.

[začít časy začínají 5400 7quad konec začátek řádku 378 čtyřhranný konec konec ]

Teď si pamatujte, že nám zbývají dvě nezapočítané nuly. Prostě je posuneme dolů za čáru.

[začít časy začínají 5400 7quad konec začátek řádku 37800 konec konec ]

Výsledkem je: 5400×7=37800

Nemáte čas se sami rozhodovat?

Naši odborníci vám pomohou!

Jak vynásobit sloupcem, pokud jsou v příkladu dvě víceciferná čísla

Abychom pochopili, jak násobit víceciferná čísla ve sloupci, vezměme si úlohu a zvažme algoritmus pro její řešení. Řekněme, že potřebujeme vynásobit 8063 číslem 207.

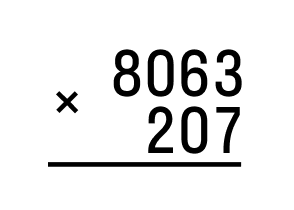
Prvním krokem je správné zapsání činitelů. Činitel s více číslicemi se zapíše jako první. V našem případě 8063. Druhý činitel se zapíše pod něj – 207. Nezapomeňte na striktní dodržování číslic. Pokud musíme řešit příklady, ve kterých mají oba činitelé stejný počet číslic, lze je zapsat v libovolném pořadí.

Dalším krokem je násobení jednotek. To znamená, že vynásobíme 3 číslicí 7, poté 6 číslicí 7 a tak dále, všechny číslice prvního multiplikátoru jednotkami druhého. Získaný výsledek bude považován za meziprodukt. V některých zdrojích se nazývá neúplný součin.

Dalším krokem je násobení desítek. Protože máme v desítkách druhého dělitele nulu, jednoduše ho přeskočíme. Podle pravidel při násobení nulou stále dostaneme nulu.

Dalším krokem je násobení stovek. Výsledkem je druhý neúplný součin nebo druhý mezivýsledek. Ten by měl být zapsán pod první mezivýsledek, jak je znázorněno níže.

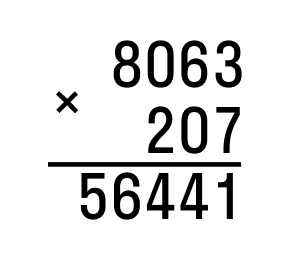
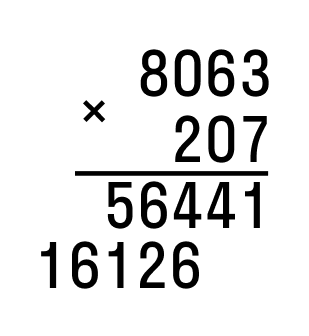
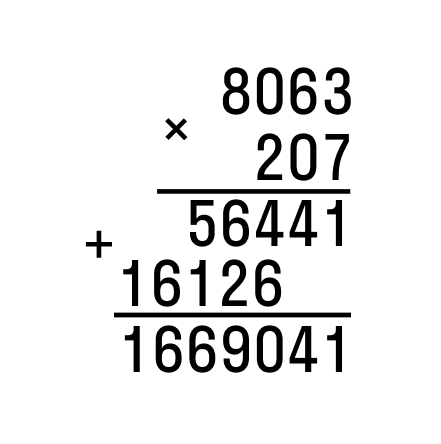
Pod čáru zapíšeme sedmiciferný výsledek získaný sčítáním, který bude odpovědí.

Můžeme tedy zapsat výraz:

Dá se říci, že pro rychlé a správné řešení úloh na násobení ve sloupci je nutné dokonale znát násobilku, pamatovat si pravidla sčítání ve sloupci a také si pamatovat základní matematické pojmy.

Následující pojmy se chápou jako základní:

• Jednociferné číslo – je číslo skládající se z jedné číslice (například 6).
• Dvoumístné číslo – toto je číslo, které obsahuje dvě přirozená čísla (například 28) atd.
• Uvolnění – je pozice, kterou číslo zaujímá v kombinaci s jinými čísly. Číslice se počítá od konce.
• Jednotky číslice – je konec libovolného víceciferného čísla. Před ním je místo desítek, poté místo stovek atd.

Například číslo 4657.

7 – číslice jednotek;

6 – místo pro stovky;

Násobení – je aritmetická operace, při které se násobí dvě složky – činitelé. Výsledek této operace se nazývá součin.

Abyste pochopili, jak řešit násobení ve sloupcích, musíte si pamatovat základní pravidla této matematické operace.

1. Změna pořadí faktorů neovlivní výsledek.
   [x krát y = y krát x]
2. Součin tří nebo více činitelů bude mít stejnou hodnotu, i když je libovolná skupina nahrazena tímto součinem.
   [x krát y krát z = (x krát y) krát z]
3. Násobení nulou vždy vrátí nulu.

Existuje ještě jedna kategorie příkladů, které stojí za pozornost. Jedná se o násobení činitelů, z nichž každý má na konci nuly. V takových příkladech se často dělají chyby. Bez ohledu na počet nul na konci víceciferných přirozených čísel je třeba postupovat v pořadí popsaném v níže uvedeném příkladu.

Příklad násobení čísel ve sloupci

Podmínka: 34500 × 230

První věc, kterou musíte udělat, je napsat příklad do sloupce tak, aby přirozená čísla jiná než nula byla umístěna jedno pod druhým.

Jakmile máme příklad zapsaný do sloupce, můžeme jednoduše vynásobit faktory podle
pravidla pro násobení víceciferných čísel bez započítání nul.

Během výpočtů bychom měli dostat dva neúplné nebo mezivýsledky.

Posledním krokem je sečtení dvou mezivýsledků a přepsání nul vpravo. Zapíšeme tolik nul, kolik jich mají oba činitelé, tedy tři.

Výsledkem je, že 34 500 × 230 = 7 935 000

Analýzou výše uvedeného příkladu můžeme říci, že libovolná čísla bez výjimky lze vynásobit ve sloupci, pokud se budeme řídit pravidly matematiky. Násobení dvouciferných čísel ve sloupci je školní program, po jehož zvládnutí se každé dítě, žák čtvrté třídy, naučí řešit příklady.

Podívejme se, jak násobit dvouciferná čísla pomocí tradičních metod, které se učíme ve škole. Některé z těchto metod vám s dostatečným procvičováním umožní rychle násobit dvouciferná čísla z hlavy. Znalost těchto metod je užitečná. Je však důležité si uvědomit, že to je jen špička ledovce.

Tato lekce se zabývá nejoblíbenějšími technikami násobení dvouciferných čísel.

Obsah:

• Rozložení do desítek a jednotek
• Aritmetické úpravy
• Mentální vizualizace násobení v dlouhém pořadí

Začněme s tím nejjednodušším.

Rozložení do desítek a jednotek

Nejjednodušší způsob, jak pochopit, jak násobit dvouciferná čísla, je ten, který nás učili ve škole. Spočívá v rozložení obou činitelů na desítky a jednotky a následném vynásobení výsledných čtyř čísel. Tato metoda je poměrně jednoduchá, ale vyžaduje schopnost zapamatovat si až tři čísla najednou a zároveň provádět aritmetické operace.

Například: 63*85 = (60+3)*(80+5) = 60*80 + 60*5 +3*80 + 3*5=4800+300+240+15=5355

Takové příklady se řeší jednodušeji ve 3 krocích. Nejprve se desítky vynásobí navzájem. Poté se sečtou 2 součiny jednotek a desítek. Nakonec se sečte součin jednotek. Schematicky lze to popsat následovně:

• První krok: 60*80 = 4800 – nezapomeňte
• Druhý krok: 60*5+3*80 = 540 – nezapomeňte
• Třetí akce: (4800+540)+3*5= 5355 – odpověď

Výstup. Není těžké vidět, že tato metoda není nejúčinnější, to znamená, že umožňuje dosáhnout správného výsledku s nejmenším úsilím. Je třeba zvážit i jiné metody.

Aritmetické úpravy

Převedení příkladu do pohodlné formy je poměrně běžný způsob mentální aritmetiky. Úprava příkladu je vhodná, když potřebujete rychle najít přibližnou nebo přesnou odpověď. Touha upravit příklady podle určitých matematických vzorců se často pěstuje na katedrách matematiky na univerzitách nebo ve školách v hodinách s matematickým zaměřením. Lidé se učí nacházet jednoduché a pohodlné algoritmy pro řešení různých problémů. Zde je několik příkladů úprav:

Příklad 49*49 lze vyřešit takto: (49*100)/2 – 49. Nejprve se 49 vypočítá děleno stovkou – 4900. Poté se 4900 vydělí dvěma, což se rovná 2, a poté se odečte 2450. Celkem je to 49.

Součin 56*92 se řeší takto: 56*100 – 56*2*2*2. Ukazuje se: 56*2 = 112*2 = 224*2 = 448. Odečteme 5600 od 448, dostaneme 5152.

Tato metoda může být efektivnější než předchozí pouze tehdy, pokud máte mentální aritmetiku založenou na násobení dvouciferných čísel jednocifernými a dokážete si uchovat v paměti několik výsledků současně. Kromě toho musíte strávit čas hledáním algoritmu řešení a velká pozornost se věnuje správnému dodržování tohoto algoritmu.

Výstup. Metoda, kdy se snažíte vynásobit 2 čísla jejich rozložením na jednodušší aritmetické postupy, dobře trénuje váš mozek, ale je spojena s větší mentální námahou a riziko špatného výsledku je vyšší než u první metody.

Mentální vizualizace násobení v dlouhém pořadí

56*67 – počítejme ve sloupci.

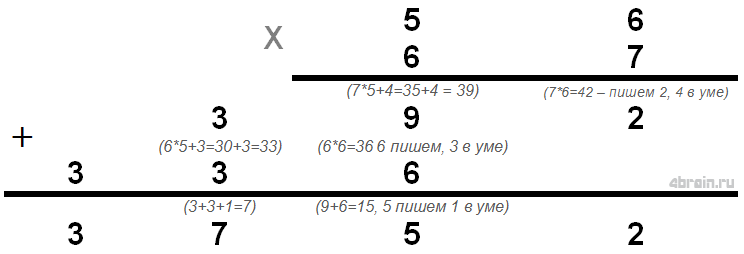
Počítání ve sloupcích pravděpodobně obsahuje maximální počet akcí a vyžaduje neustálé pamatování na pomocná čísla. Lze to ale zjednodušit. Ve druhé lekci bylo vysvětleno, že je důležité umět rychle násobit jednociferná čísla dvoucifernými. Pokud to už umíte dělat automaticky, pak pro vás násobení ve sloupci z hlavy nebude tak obtížné. Algoritmus je následující.

První dějství: 56*7 = 350+42=392 – pamatujte si to a nezapomeňte až do třetího dějství.

Druhé dějství: 56*6=300+36=336 (ну или 392-56)

Třetí dějství: 336*10+392=3360+392=3 – tohle je složitější, ale můžete začít pojmenovávat první číslo, kterým si jste jistí – „tři tisíce…“, a při mluvení sečíst 752 a 360.

Závěr: Počítání sloupců je přímo obtížné, ale můžete si ho zjednodušit, pokud umíte rychle násobit dvouciferná čísla jednocifernými. Přidejte si tuto metodu do svého arzenálu. Ve zjednodušené podobě je počítání sloupců modifikací první metody. Která je lepší, je otázkou vkusu.

Jak vidíte, žádná z výše popsaných metod vám neumožňuje dostatečně rychle a přesně mentálně spočítat všechny příklady násobení dvouciferných čísel. Je důležité si uvědomit, že použití tradičních metod násobení pro mentální počítání není vždy racionální, tj. umožňuje dosáhnout maximálních výsledků s nejmenším úsilím.

Dále se budeme zabývat konkrétními metodami.