Ešení základních topografických problémů | PermaWiki | Fandom
Chcete-li změřit vzdálenost na mapě, vezměte ji pomocí kompasu a přeneste ji do lineárního měřítka umístěného pod jižním rámem mapy.
Přesněji se vzdálenost měří pravítkem s milimetrovými dílky. Údaj pravítka, vyjádřený v centimetrech, se vynásobí počtem metrů uvedeným v pojmenovaném měřítku mapy.

Ještě přesnější měření se provádí pomocí příčné stupnice. Na kovovém pravítku skrz m intervaly, jsou vyryty rovnoběžné čáry – horizontály (obvykle m = 10). K nim se přidávají kolmice – svislice, jejichž vzdálenost se nazývá základna stupnice d (obvykle d = 2 cm). Levá základna je rozdělena na n části a protaženy získanými body n šikmé čáry – příčné (obvykle n = 10 nebo 5). Délky segmentů rovnoběžných se základnou jsou stejné v příčném měřítku: mezi sousedními vertikálami – d, mezi sousedními příčkami – d/n. Délky segmentů mezi vertikálou a transverzálou vycházejícími ze stejného bodu se liší od 0 do d/n. Nejmenší dílek příčné stupnice, který určuje její přesnost, je roven d/(mn).
Pro snadné použití jsou příčné dělení měřítka základny a horizontály digitalizováno v souladu s měřítkem plánu. Digitalizace na obrázku odpovídá měřítku 1:500.
Chcete-li změřit vzdálenost, vezměte ji do roztoku měřicího kompasu. Jeho pravá noha je umístěna na jedné ze svislic příčné stupnice a levá noha je umístěna na jedné z příčných, ale tak, že obě nohy jsou ve stejné horizontále. Naměřená vzdálenost se rovná součtu vzdáleností odpovídajících počtu celých základen, desetin základny a setin pokrytých řešením kompasu, odhadnuté podle polohy ramena kompasu na transversále. Na obrázku je segment ab má délku 20+3+0,7=23,7m Délka segmentu cd je rovna 30+5+0,45=35,45 m Z druhého příkladu je zřejmé, že délku segmentu lze měřit s přesností poloviny nejmenšího dílku (v tomto případě 0,05 m).
K měření délek navíjecích šňůr se používá speciální zařízení – křivoměr, vybavený kolečkem, které se odvaluje po měřené šňůře. Otáčení se přenáší na ručičku číselníku, ze které se odečítá naměřená vzdálenost.
Určení souřadnic bodů [ ]
K určení zeměpisných souřadnic se používá minutový snímek mapy. Přes kulaté hodnoty v minutách zeměpisné šířky je nakreslena čára na západním a východním snímku jižně od určeného bodu. Vezmeme kompas pro měření vzdálenosti а z definovaného bodu M k nakreslené čáře, položte ji na rám mapy a pomocí desetisekundových dělení vypočítejte počet sekund.
K určení zeměpisné délky je na severním a jižním snímku nakreslena svislá čára přes stejné minuty. Vzdálenost od bodu k přímce se přenese s metrem na severní nebo jižní rám a vypočítá se počet sekund.
Pravoúhlé souřadnice jsou určeny pomocí kilometrové sítě, jejíž čáry jsou rovnoběžné se souřadnicovými osami x и y. Souřadnice bodu P jsou určeny vzorcem
kde xю и yз— hodnoty souřadnic na čarách mřížky procházejících jižně a západně od bodu Р. Jsou označeny (v kilometrech), kde čáry vystupují z rámu. Segmenty Dx и Dy opatření.
Zvyšte přesnost určování souřadnic bodů Р možné měřením vzdáleností a и b na nejbližší jižní a severní čáru mřížky, stejně jako vzdálenost c и d k nejbližší západní a východní mřížce. Segmenty Dx и Dy, vyjádřené v metrech, se vypočítají pomocí vzorců
Δx = 1000 a / (a + b), Δy = 1000 XNUMX c / (c + d), (4.1)
kde násobitel 1000 je délka strany čtverce kilometrové sítě v metrech.
Dodatečný efekt měřicích segmentů abeceda a použití vzorců (4.1) má snížit chyby způsobené deformací papíru. Stejnou techniku lze použít při určování zeměpisných souřadnic.
Definování úhlů orientace [ ]
Směrový úhel směru segmentu na mapě se měří pomocí úhloměru jako úhel měřený ve směru hodinových ručiček od severního směru čáry kilometrové mřížky ke směru segmentu. V případě potřeby se před měřením segment prodlouží, dokud se neprotne s čárou mřížky.
K určení azimutu А směry nejprve změří jeho směrový úhel a. Poté se vypočítá azimut: A=a+gKde g – konvergence poledníků, jejichž význam je podepsán pod jižním rámem mapy a je znázorněn na zde umístěném diagramu.
Můžete také přímo měřit azimut. Svislá čára je nakreslena přes stejné hodnoty minut zeměpisné délky – poledník. Úhel mezi severním směrem poledníku a směrem segmentu je azimut.
Deklinace magnetické střelky je také vyznačena pod jižním rámem mapy a na schématu. d, který umožňuje vypočítat azimut magnetického směru pomocí vzorce Ам = A – d.
Stanovení výšek bodů [ ]
Výška bodu ležícího na horizontále se rovná výšce horizontály. Výšky jednotlivých vodorovných čar jsou označeny u jejich zlomu. Výšky ostatních vrstevnic lze snadno zjistit, když znáte výšku řezu reliéfu, jakož i výšky podepsaných vrstevnic a výšky těch charakteristických bodů reliéfu, na kterých jsou podepsány jejich značky. V tomto případě se bere v úvahu, že výšky vrstevnic jsou násobky výšky reliéfního úseku.
Výška bodu Mumístěný mezi dvěma vodorovnými čarami je určen vzorcem
kde Hг – výška menší horizontály, h je výška reliéfní sekce a segmentů a и b – poloha svahu a vzdálenost od bodu k vodorovné rovině, měřená na mapě pravítkem.
Vytvoření profilu [ ]
Chcete-li sestrojit profil podél čáry nakreslené na mapě, určete výšky bodů v místech, kde se protíná s vodorovnými čarami, rozvodnicemi a odvodňovacími čarami. Změřte k nim vodorovné vzdálenosti od počátečního bodu úsečky. Při konstrukci profilu se vzdálenosti vykreslují podél vodorovné osy a výšky podle svislé osy. Pro přehlednost je vertikální měřítko bráno větší než horizontální (10krát nebo dokonce 50krát).
Určení sklonů a úhlů sklonu [ ]
Úsečky na zemském povrchu mají obvykle sklon, proto je začátek a konec úseku v různých výškách. Rozdíl v jejich výškách je přebytek a průmět segmentu na vodorovnou rovinu je jeho horizontální umístění.
Sklon i čára se nazývá přebytečný poměr h k horizontální instalaci d:
i=h/d (4.2)
Určení sklonu čáry na místě pomocí mapy KL (viz obrázek) mezi dvěma vodorovnými čarami změřte jeho vodorovnou polohu – položení d. Protože konce segmentu leží na sousedních vodorovných liniích, přebytek h mezi nimi je rovna výšce reliéfního řezu, podepsaného pod jižním rámem mapy. Pomocí vzorce (4.2) se vypočítá sklon, který se obvykle vyjadřuje v tisícinách. Pokud např. h= 1 m, d=48 m, pak je sklon i =1 m / 48 m = 0,021 = 21‰.
Na druhou stranu přebytečný poměr h k horizontální instalaci d rovna tečně úhlu n sklon čáry. Proto
i = tg n,
který umožňuje výpočtem sklonu z něj určit úhel sklonu.
Při použití mapy se úhly sklonu nepočítají, ale určují se pomocí výškového grafu umístěného pod jižním rámem mapy. Vodorovná osa grafu ukazuje úhly sklonu a svislá osa ukazuje úhly odpovídající těmto úhlům. d, vyjádřené v měřítku mapy a vypočtené vzorcem
d = h(M tg n),
kde h je výška reliéfní části a M – jmenovatel měřítka mapy.
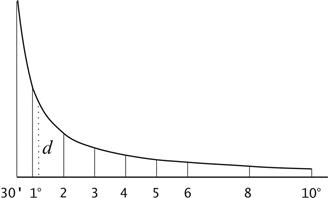
K určení úhlu sklonu segmentu KL (viz obrázek) umístěný mezi vodorovnými čarami, vezměte jej do řešení kompasu a na vykreslovacím grafu najděte úhel, nad kterým je pořadnice rovna řešení kompasu d. Toto je požadovaný úhel sklonu.
Pokud je nutné opakovaně určit sklony, použijte graf sklonu vytvořený podobně jako graf vynesení, ale se sklony spíše než s úhly sklonu vynesenými podél vodorovné osy.
Kreslení čáry se sklonem nepřesahujícím stanovený limit [ ]

Potřeba řešit takový problém vyvstává například při výběru trasy pro budoucí komunikaci. Vypočítejte odpovídající maximální sklon iпр místo vyjádřené v měřítku mapy,
d = h / (M * iпр) (zde M je jmenovatel stupnice).
Aby se zajistilo, že sklon čáry nepřekročí ipr, žádná poloha na ní by neměla být menší než vypočtená d. Pokud je vzdálenost mezi vodorovnými čarami větší než vypočítaná, lze směr čáry zvolit libovolně. V opačném případě vezměte do kompasového řešení úsečku rovnající se d a vytvořte přerušovanou čáru, přičemž vypočítanou mezní polohu umístěte mezi vodorovné čáry (obr. 4.9).
Určení hranic povodí (povodí) [ ]
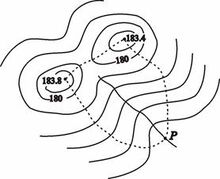
Povodí je oblast, ze které stéká dešťová a tající voda do daného koryta. Určení drenážní plochy je nutné např. při návrhu komunikace pro výpočet otvoru mostu nebo potrubí.
Pro určení hranic povodí se do mapy zakreslují čáry povodí a poté se od navržené konstrukce k čarám povodí kreslí čáry největšího sklonu kolmé k vodorovným čarám.
Například odvodňovací plocha pro bod P, kde má být potrubí vybudováno (obr. 4.10), je ohraničeno čárkovanou čarou tvořenou povodím a dvěma čarami největšího sklonu.
Prameny [ ]
- http://studopedia.ru/2_14769_reshenie-zadach-po-topograficheskoy-karte.html
- http://www.minskgreen.by/Books/Atroshko_geod.pdf